Reinforcement Learning Parte 1 - Introdução
Esta é a primeira parte de uma série de posts nos quais vamos concentrar nossa atenção em uma parte de Machine Learning (ML) chamada Aprendizado por Reforço. Esta talvez seja a parte menos conhecida de ML e é aquela que possui maior semelhança com os métodos que humanos e animais usam para aprender a realizar tarefas, e ela inicialmente também envolve uma menor abstração matemática para entender o funcionamento dos algoritmos.
A intenção desta série é apresentar e explicar desde os princípios básicos até a demonstração do funcionamento dos principais algoritmos. Para isso, vamos utilizar um pouco de matemática (tentarei explicar o melhor possível, prometo!) e Python. Se você procurar em vários lugares (como o Medium) verá que quase sempre há referência ao livro Reinforcement Learning An Introduction, dos autores Richard S. Sutton e Andrew G. Barto, pois é o livro mais influente nessa área e, na minha opinião o melhor lugar para se começar. Os dois autores possuem uma longa carreira pesquisando sobre Aprendizado por Reforço e ao longo do livro apresentam bem todas as características dos artigos e propõem vários pequenos problemas a serem resolvidos. Essa obra será também nossa principal referência.
Devido à forte influência do livro a OpenAi criou o Gym, um toolkit de ambientes (em Python) baseados nos problemas sugeridos no livro. Esses ambientes (environments) simulam as situações propostas para que pesquisadores, estudantes e curiosos possam testar e comparar seus algoritmos sem se preocupar com o ambiente. Portanto, vamos nos aproveitar da facilidade e boa parte das aplicações que usaremos utilizará esses ambientes.
O que é Aprendizado por Reforço?
Em Machine Learning, os tipos de abordagens de problemas se dividem em três classes: Aprendizado Supervisionado (Supervised Learning); Aprendizado Não-Supervisionado (Unsupervised Learning); e Aprendizado por Reforço (Reinforcement Learning ou RL). Para ilustrar, usamos uma imagem retirada daqui:
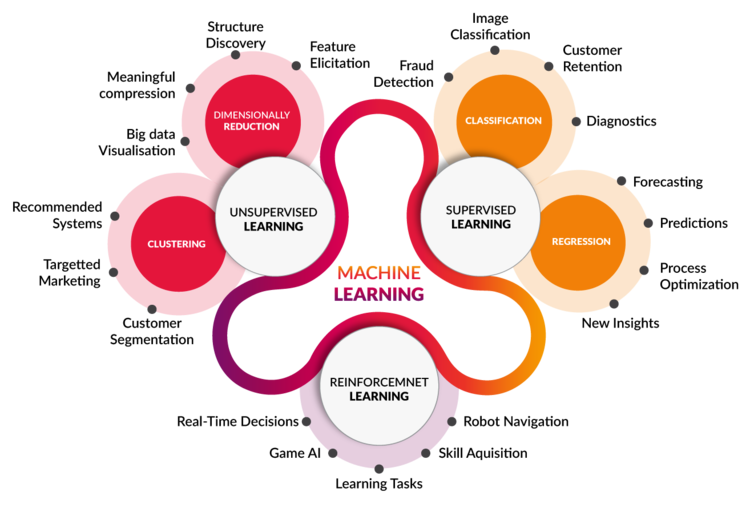
Em RL, podemos sempre imaginar que temos um robô dentro de um jogo ou mundo. O objetivo dele é aprender como vencer o jogo de maneira ótima (mais pontos, menor tempo, com mais vidas sobrando, etc). Para indicar como o robô está se saindo durante as jogadas ele precisa de algum tipo de indicação sobre seu comportamento, ou seja, existe uma espécie de pontuação recebida como recompensa quando uma ação boa é executada. Damos os nomes de agente (agent) ao robô e ambiente (environment) ao jogo dentro do qual ele se encontra.
Bom, vamos imaginar um jogo bem simples: nosso agente (O) está dentro de um labirinto que contém armadilhas (T) e a saída (X):
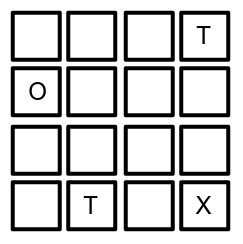
As regras são as seguintes:
- o agente inicia em um quadrado aleatório desde que não seja a saída ou uma das armadilhas;
- o movimento possível é andar para um quadrado adjacente ao que ele está, então na imagem acima ele não pode andar para a esquerda;
- se o movimento resultar em uma posição que não é armadilha ou saída, o agente pode se mover mais uma vez;
- se o movimento levá-lo a uma armadilha, o agente perde a partida (perde uma vida) e deve iniciar novamente;
- se o movimento levá-lo ao quadrado da saída, ele vence a partida.
Se você já viu algo sobre esse assunto deve ter se deparado com vários termos como “agente”, “retorno”, “recompensa”, “estado”, entre outros. Para nos acostumarmos com o que virá, vamos deixar claro desde já os principais termos que usaremos por aqui.
Action (A)
Action (ação) é o conjunto de movimentos ou jogadas que o agente pode executar. Uma ação qualquer dentro das possíveis é usualmente denotada como $a \in A$. Ex: no labirinto, o agente pode ter no máximo 4 ações diferentes: andar para cima, baixo, esquerda ou direita. Em alguns momentos as quatro ações podem estar disponíveis, em outros, apenas três ou duas.
State (S)
State (estado) é a situação na qual o agente está dentro do ambiente. Um estado qualquer dentro dos possíveis é usualmente denotado como $s \in S$. Ex: no labirinto o estado é simplesmente a posição ou o quadrado ocupado pelo agente. Os quadrados com armadilhas ou saída são chamados de estados terminais (terminate states), pois causam o término da partida.
Reward (R)
Reward (recompensa) é uma quantidade numérica fornecida ao agente quando este executa ações que o levam a vencer o jogo ou são apenas consideradas boas. A recompensa é dada na maioria dos casos por ações executadas recentemente, geralmente a última. Ex: no nosso problema nós definimos quando o robô ganha uma recompensa, pode ser apenas quando vence uma partida ou até mesmo quando se aproxima dela. Funciona como uma espécie de medida de quão próximo o agente está de cumprir o objetivo.
Policy ($\pi$)
Policy (política) é a estratégia empregada pelo agente para escolher as ações baseado no estado em que ele se encontra. Ela é uma parte importante da modelagem do problema. Em muitos casos, não há nenhum tipo de estratégia clara e se costuma utilizar uma policy aleatória. Ex: além do movimento aleatório, poderíamos informar ao agente algo como “se o movimento para a cima não é permitido, ande para baixo”, ou mesmo: “na dúvida, use um movimento que irá para a direita ou para baixo com a mesma probabilidade”.
Value (V)
Value (valor), também chamado de state-value, é definido como o valor esperado do retorno (uma espécie de recompensa) a longo prazo. Basicamente, isso seria o valor médio de recompensa ganha no fim da partida associado a um determinado estado. Ex: no labirinto, um quadrado ao lado da saída e longe de armadilhas tem uma chance maior de levar o robô a vencer a partida do que um quadrado ao lado de uma armadilha e longe da saída. Assim, se o valor dos estados for conhecido, o robô pode optar por ir para o estado que tem maior valor.
Q-value (Q)
Também conhecido como action-state-value, é similar ao state-value, porém associado à recompensa de curto prazo. Dado um estado que disponibiliza mais de uma ação possível, aquelas que levam o agente a vencer a partida têm um valor maior que as demais. Ex: na imagem abaixo, o agente está em um estado ($s_{3,4} = s_{linha\ 3, coluna\ 4}$) que permite as ações $a_{cima}$, $a_{esquerda}$ e $a_{baixo}$. Vemos que a última leva à saída e a primeira a um estado próximo de perder, portanto, os valores de cada ação possivelmente respeitariam a seguinte relação: $Q(s_{3,4},a_{baixo}) > Q(s_{3,4},a_{esquerda}) > Q(s_{3,4},a_{cima})$.
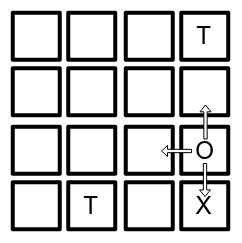
Step e Episode
Step determina uma passagem de tempo; usualmente, cada vez que o agente executa uma ação se passa um step. Ex: podemos considerar o step no labirinto quase que literalmente como um passo, pois quando o agente “anda” para um quadrado adjacente ele usa um step.
Episode é uma partida completa. Pode durar um número fixo de steps ou ser variável. Ex: sempre que o estado é igual a uma armadilha ou saída, um episódio é encerrado.
Conclusão
Conhecendo um pouco da nomenclatura já podemos ter uma ideia do que acontece em RL. Se nos foi dada a tarefa de criar um agente que é capaz de sair deste labirinto, nosso verdadeiro objetivo é utilizar algum método (veremos quais) que é capaz de aprender qual é a optimal policy, ou seja, qual é a estratégia que fará o agente vencer o maior número possível de partidas, não importando em que estado ele inicie.
Para problemas simples como o nosso, existe tal estratégia (pode existir mais de uma) e nós, humanos, conseguimos encontrá-la facilmente, como mostramos na figura abaixo. Já ensinar um robô pode não ser tão simples.
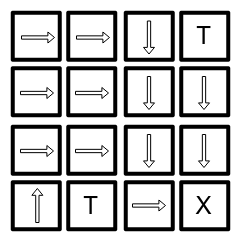
Para problemas mais complexos, como sair de um labirinto dinâmico, jogar xadrez, dirigir um carro ou jogar em um cassino não há tal garantia e, portanto, procuramos uma policy que seja aproximadamente ótima. A maneira que os algoritmos utilizam para resolver os problemas gira em torno de técnicas para estimar state-values e action-state-values através da experiência adquirida pelo agente ao longo dos episódios.
Nossa missão nos próximos posts é utilizar essas técnicas para resolver vários problemas. No próximo post, vamos justamente abordar a técnica conhecida como Q-Learning para ensinar nosso robô a fugir de um labirinto parecido com o que vimos, mas que possuirá um risco extra, pois o agente andará sobre o gelo.
